来源 https://zhuanlan.zhihu.com/p/455171966
算法在并行环境中的性能通常由必须共享的状态数量来决定。如果多个Python进程之间没有互相通信(可以认为没有共享状态),那么通信开销并不大;如果每一个进程都需要和其他所有Python进程之间通信,那么通信开销会比较大,事情的处理会越来越慢,最终使整体性能下降。
Python用于单核,实现有效的并行化会比较困难。当我们使用n个核心来解决问题时,我们的速度理论上可以达到原来的n倍。所以为了达到更好的加速,这篇文章会用两个例子探讨使用多核的方法。
multiprocessing模块能让我们使用基于进程和基于线程的并行处理,在队列上共享任务和在进程间共享数据:
- 用进程或池对象并行化一个任务。
- 用哑元模块在线程池中并行化一个I/O任务。
- 用队列共享捎带的工作。
- 在并行工作者之间共享状态(如字节、原生数据类型、字典和列表)。
先做一些名词上的解释,在multiprocessing中:
- 进程:一个当前进程的派生(forked)拷贝,创建了一个新的进程标识符,并且任务在操作系统中以一个独立的子进程运行。
- 池:包装了进程或线程。在一个方便的工作者线程池中共享一块工作并返回聚合的结果。
- 队列:一个先进先出(FIFP)的队列,允许多个生产者和消费者。
- 管理者:一个单向或双向的在两个进程间的通信渠道。
- ctypes:允许在进程派生(forked)后,在父子进程间共享原生数据类型(例如,整型数、浮点数和字节数)。
- 同步原语:锁和信号量在进程间同步控制流。
看例子。
估算pi
我们使用蒙特卡洛办法估算pi。我们将10000000个随机点放入长为2的正方形中,如果点的坐标满足:
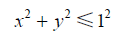
则表示点就落入到单位圆中,反之则落到圆外。由此我们可以估算出3位小数可靠的pi值。


使用Python写一个循环来实现这一过程:
import random
#用循环估计pi
def calculate_pi(nbr_estimates):
sum_trials = 0
for step in range(int(nbr_estimates)):
x = random.uniform(0,1)
y = random.uniform(0,1)
in_unit_circle = x*x + y*y <= 1.0
sum_trials += in_unit_circle
return sum_trials
使用multiprocessing导入进程池,我们创建一个包含nbr_estimates 的列表,被工作者的数量整除。它会将参数送给每一个工作者。执行后,我们会收到相同数量的返回结果,把这些结果累加起来去估算单位圆内的点数量。
if __name__ == "__main__":
from multiprocessing import Pool
import time
nbr_samples = 1e8
parallel_blocks = 4#进程数量
pool = Pool(processes = parallel_blocks)#使用multiprocessing.Pool创建进程池
nbr_samples_per_worker = nbr_samples/parallel_blocks
print("Making {} samples per work".format(nbr_samples_per_worker))
nbr_trials_per_process = [nbr_samples_per_worker]*parallel_blocks
start = time.time()
#map是同步阻塞执行,即上一个子进程结束后才能进行下一个子进程。
#iterable可迭代类型,将iterable中每个元素作为参数应用到func函数中,返回list
nbr_in_unit_circles = pool.map(func = calculate_pi,iterable = nbr_trials_per_process)
pi_estimate = sum(nbr_in_unit_circles)*4/nbr_samples
print("Estimated pi",pi_estimate)
print("Delta: ",time.time()-start)
下表列出了随着使用进程数与运行时间的关系:
| 进程数 | 1 | 2 | 4 | 6 | 8 | 16 |
| Samples per work | 1e8 | 5e7 | 2.5e7 | 1.66e7 | 1.25e7 | 6.25e6 |
| 时间 | 49.227 | 24.015 | 12.145 | 9.426 | 8.440 | 7.460 |
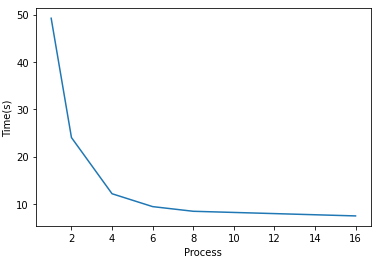
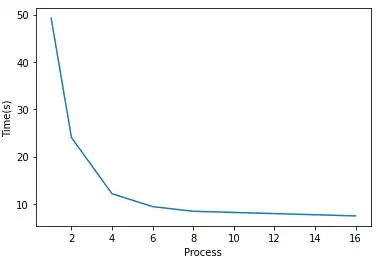
从单进程到6个线程,每增加一倍的线程,速度也会相应提升近一倍。当达到8进程和16进程时,速度提升越来越小。这可能是因为我是在六核CPU的linux系统上运行的,6个超线程几乎榨干了CPU的所有性能,几乎已经最大化利用6个CPU了。
现在我们使用一个进程中的多线程(将from multiprocessing import Pool改成from multiprocessing.dummy import Pool就能得到线程版本):
if __name__ == "__main__":
from multiprocessing.dummy import Pool
import time
nbr_samples = 1e8
parallel_blocks = 2#线程数量
pool = Pool(processes = parallel_blocks)
nbr_samples_per_worker = nbr_samples/parallel_blocks
print("Making {} samples per work".format(nbr_samples_per_worker))
nbr_trials_per_process = [nbr_samples_per_worker]*parallel_blocks
start = time.time()
nbr_in_unit_circles = pool.map(func = calculate_pi,iterable = nbr_trials_per_process)
pi_estimate = sum(nbr_in_unit_circles)*4/nbr_samples
print("Estimated pi",pi_estimate)
print("Delta: ",time.time()-start)
| 线程数 | 1 | 2 | 4 | 6 | 8 | 16 |
| Samples per work | 1e8 | 5e7 | 2.5e7 | 1.66e7 | 1.25e7 | 6.25e6 |
| 时间 | 48.551 | 48.724 | 53.873 | 56.326 | 57.118 | 58.30 |
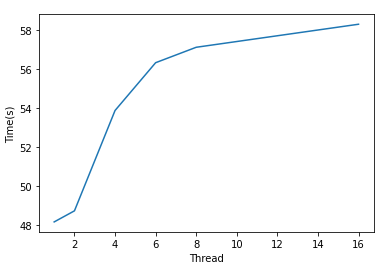
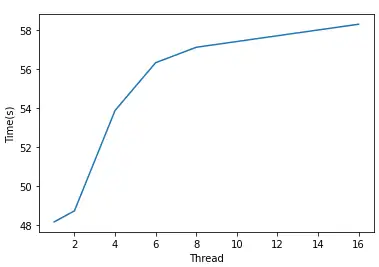
多进程中运行了一定数量的Python进程,每个进程都有自己的内存空间等,所以没有GIL竞争。而对一个进程的多线程,会存在GIL竞争而造成额外开销,于是代码运行会变慢。


此外,每当一个线程被唤醒并设法获得GIL时,就使用了系统资源。如果一个线程忙碌,那么其他线程将重复不断地唤醒并设法获取GIL,这些重复造成开销越来越大。当然,这是多线程运行于多个CPU上的问题,多线程的单核CPU没有没有GIL竞争。
我们知道,numpy因在RAM的连续块以低层次创建和操控相同的对象类型而更快,对缓存更加友好。我们使用numpy来解决上面的问题,查看速度提升。使用numpy估算pi(矢量化版本):
import numpy as np
def calculate_pi(nbr_samples):
np.random.seed()#在每个新进程中为 numpy 设置随机种子,否则folk将意味着它们都共享相同的状态k将意味着它们都共享相同的状态k将意味着它们都共享相同的状态k将意味着它们都共享相同的状态
xs = np.random.uniform(0, 1, nbr_samples)
ys = np.random.uniform(0, 1, nbr_samples)
estimate_inside_quarter_unit_circle = (xs * xs + ys * ys) <= 1
nbr_trials_in_quarter_unit_circle = np.sum(estimate_inside_quarter_unit_circle)
return nbr_trials_in_quarter_unit_circle
进程版本(包括串行和多进程)运行:
if __name__ == "__main__":
from multiprocessing import Pool
import time
nbr_samples = 1e8
parallel_blocks = 1#进程数量
pool = Pool(processes = parallel_blocks)
nbr_samples_per_worker = nbr_samples/parallel_blocks
print("Making {} samples per work".format(nbr_samples_per_worker))
nbr_trials_per_process = [int(nbr_samples_per_worker)]*parallel_blocks
start = time.time()
nbr_in_unit_circles = pool.map(func = calculate_pi,iterable = nbr_trials_per_process)
pi_estimate = sum(nbr_in_unit_circles)*4/nbr_samples
print("Estimated pi",pi_estimate)
print("Delta: ",time.time()-start)
结果:
| 进程数 | 1 | 2 | 4 | 6 | 8 | 16 |
| Samples per work | 1e8 | 5e7 | 2.5e7 | 1.66e7 | 1.25e7 | 6.25e6 |
| 时间 | 11.382 | 4.133 | 1.220 | 0.701 | 0.643 | 0.549 |
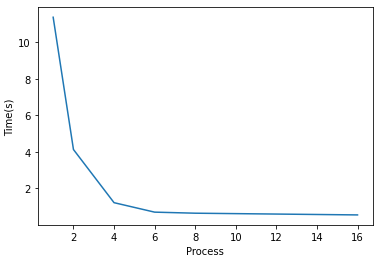
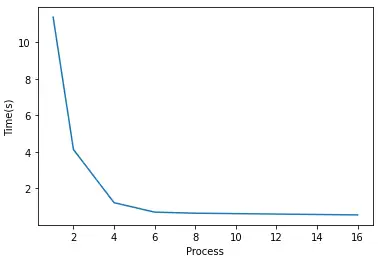
比使用纯Python版本快了很多。
使用线程版本:
if __name__ == "__main__":
from multiprocessing.dummy import Pool
import time
nbr_samples = 1e8
parallel_blocks = 1#进程数量
pool = Pool(processes = parallel_blocks)
nbr_samples_per_worker = nbr_samples/parallel_blocks
print("Making {} samples per work".format(nbr_samples_per_worker))
nbr_trials_per_process = [int(nbr_samples_per_worker)]*parallel_blocks
start = time.time()
nbr_in_unit_circles = pool.map(func = calculate_pi,iterable = nbr_trials_per_process)
pi_estimate = sum(nbr_in_unit_circles)*4/nbr_samples
print("Estimated pi",pi_estimate)
print("Delta: ",time.time()-start)
得到结果:
| 线程数 | 1 | 2 | 4 | 6 | 8 | 16 |
| Samples per work | 1e8 | 5e7 | 2.5e7 | 1.66e7 | 1.25e7 | 6.25e6 |
| 时间 | 9.414 | 2.169 | 1.991 | 1.943 | 1.912 | 1.976 |
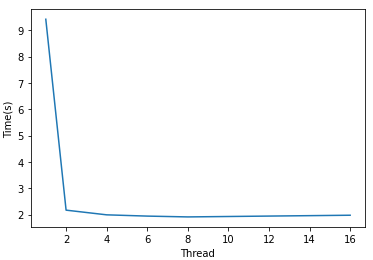
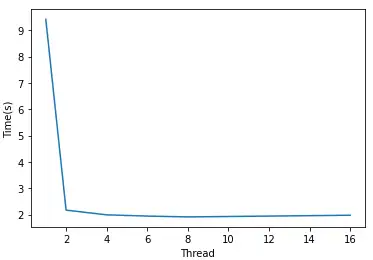
同样比纯Python快了很多,并且线程越多,速度基本会越快。通过工作于GIL之外,numpy能够用多线程达到更快的速度。
找素数
找素数是与估算pi不同的问题,因为工作负载会因数值位置而变,并且每个数字检查都有不可预测的复杂度。我们会使用调制队列来使用计算资源,并用简单的办法有效使用资源。使用Python寻找素数:
import math
def check_prime(n):
if n % 2 == 0:
return False
start = 3
end = int(math.sqrt(n))+1
for i in range(start , end, 2):
if n % i == 0:
return False
return True
当我们给进程池分配工作时,我们可以指定要给每个工作者传递的工作量。我们可以均匀地划分所有工作并力求一次传递完,或者我们也可以创建很多工作块,当CPU空闲时就把它们传递出去。
chunksize指定了工作块的大小。更大的工作块意味着更少的通信开销,而更小的工作块意味着资源分配更灵活。对找素数来说,一个单独的工作划片是一个由check_prime检测的数字n。例如chunksize是8就意味着每一个进程处理一列8个整数,同时处理一列。
为了探究工作块的影响,我们固定了进程数而改变chunksize:
if __name__ == "__main__":
from multiprocessing import Pool
import time
n = 1e8
parallel_blocks = 6#进程数量
pool = Pool(processes = parallel_blocks)
nbr_list = [int(n+i) for i in range(1000000)]
chunksize = 2#工作块的划分
start = time.time()
nbr_in_unit_circles = pool.map(func = check_prime,iterable = nbr_list,chunksize = chunksize)
print("Delta: ",time.time()-start)
我们可以看到从1(每个任务是一个单独的工作划片)到64(每个任务是一列64个数字)之间变化的chunksize的效果:
| chunksize | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
| 时间 | 31.625 | 15.052 | 7.517 | 4.834 | 3.967 | 3.592 | 4.099 | 3.775 |
尽管有小的任务能带来高的灵活性,但也强加了最大的通信开销。所有的CPU 会有效地得以利用,但是当每一个任务和处理结果都经过一个单独的通信管道传输时,这个单独的信道就变成了一个瓶颈。
把chunksize 翻2倍,任务就以两倍快的速度得到了解决,因为在通信管道上有更少的竞争,但过大的chunksize有可能会让时间变长,比如让chunkszie=50000,那么两个CPU会有空闲,从而造成低效。因此错配工作负载和可利用资源也会导致低效。
这种情况下的优化是让任务数量和CPU数量一致,即默认的chunksize。
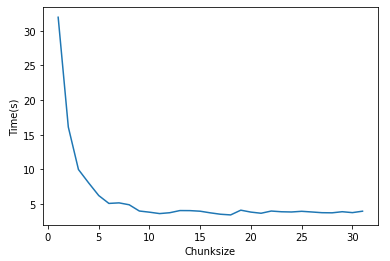
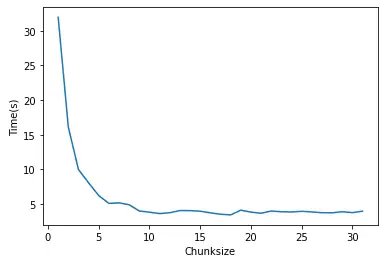
如上图所示,错配会导致低效。1到5个工作块都会使一部分CPU无法利用,6个工作块时采用上所有资源。这时如果增加了第7个工作块,那么资源会再次利用不足,因为6个CPU会工作在他们的块上,接着一个CPU将运行计算第7个块。
原创文章,转载请注明出处:http://124.221.219.47/article/891445/